平行四边形和菱形的判定和性质「初中数学|特殊平行四边形菱形的性质与判定」

菱形是一种特殊的平行四边形。在讲菱形之前，我们首先来回顾一下矩形的相关知识点。

矩形区别于一般平行四边形的特殊性质主要有两个：

1、四个角都是90°；

2、对角线相等且平分。

菱形的定义和性质：

菱形是在平行四边形的前提下定义的，我们将有一组领边相等的平行四边形叫做菱形。

那么菱形都有哪些性质呢？

菱形是特殊的平行四边形，所以它具有平行四边形的所有性质，此外菱形还有以下性质：

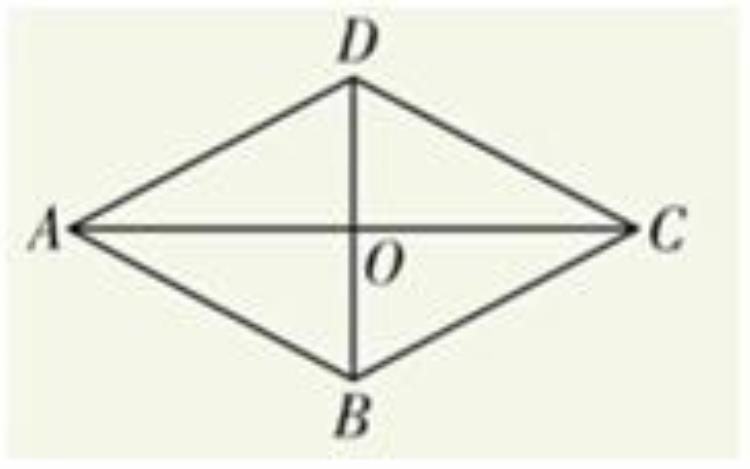
1、菱形的四条边都相等；

2、菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。

例1：如图，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为？

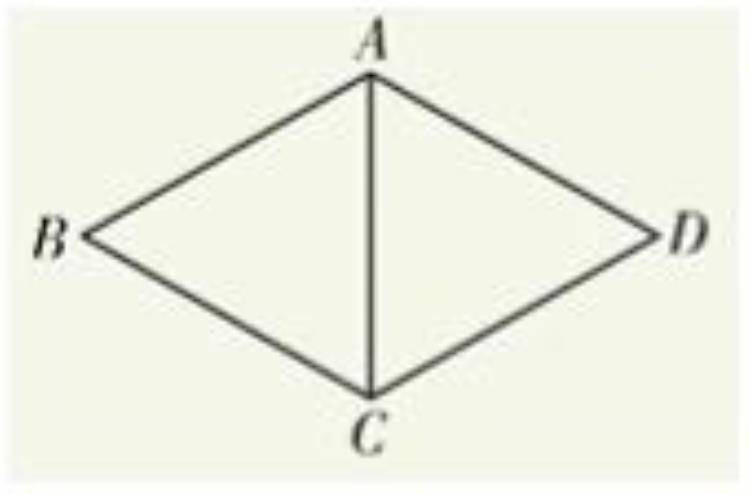
解析：

根据菱形的性质，得出∠BAC=∠DAC，

又因为菱形的邻角互补，所以∠ABC=180°-∠BAD=60°

在菱形ABCD中，AB=AC=AD=DC

故三角形ABC=ADC，且为等边三角形

因AC=4，所以菱形ABCD的周长为4X4=16。

例2：如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为？

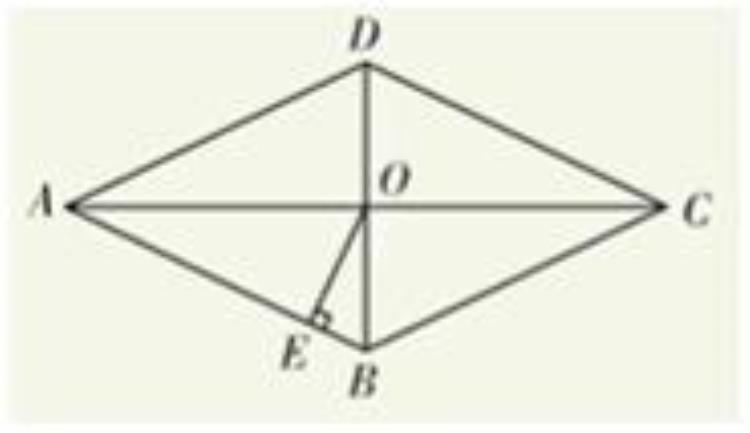
解析：

因为∠ADC=130°且BD为对角线，

所以∠ADO=∠CDO=65°

因为∠DAB为∠ADC的补角，

所以∠DAB=50°

因为AC平分∠DAB，所以∠OAE=∠OAB=25°

因为OE⊥AB

所以∠AOE=90°-25°=65°

我们来看下面这些思考题。

思考：

1、菱形的对角线把菱形分成四个直角三角形，它们是否全等？

2、菱形是不是轴对称图形？

3、由菱形的两条对角线的长，你能求出它的面积吗？

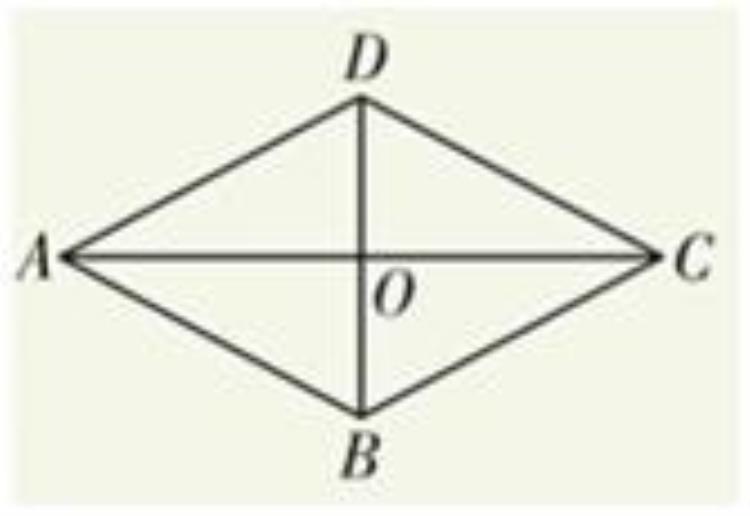
解析：

1、如图，根据菱形的性质，得AB=AD＝BC=DC，OB=OD，OA=OC。

所以三角形AOD=AOB=BOC＝DOC。

2、因为菱形是特殊的平行四边形，

所以它也是一个中心对称图形。

因为AC⊥BD，且四边相等，

所以它是轴对称图形，对称轴为AC和BD。

3、求菱形的面积，第一种方法为过AB给菱形作高DH，

S菱形ABCD=ABXDH＝底X高。

第二种方法：因为菱形ABCD中三角形ABC＝ADC，

所以S菱形ABCD＝２XXACXOD＝ACXOD=XACXBD。

其实在四边形中不止有菱形的面积为对角线乘积的一半，如果其对角线互相垂直，都可以采用这种方法。

例3：如图，菱形ABCD的对角线交于点O，AC=16cm，BD=12cm，求菱形的边长和面积。

因为菱形的对角线互相垂直且平分，所以OA=AC=X16=8(cm)。

OB=BD=X12=6(cm)，所以AB==10（cm）。

所以菱形的边长为10cm。

S菱形ABCD=4S三角形OAB=4XX6X8=96平方厘米。

今天的知识就学到这里啦，你都掌握了吗？