月球运行速度小于第一宇宙速度「月球公转速度远低于第一宇宙速度为什么不会从天上掉下来」

这是回答一位网友的问题，他说：月球的公转速度为每秒1.02公里，远低于第一宇宙速度的每秒7.9公里，按说它是不能绕地球公转的，怎么没有掉下来？想不明白。

现在我们就来说说这个问题。

所谓第一宇宙速度、第二宇宙速度、第三宇宙速度是以地球表面为前提，通过引力方程，也就是牛顿的万有引力定律计算出来的，这个定律表述为：F=MmG/r^2，其含义是引力作用大小，是与物体质量成正比，与物体之间的距离平方成反比的。

也就是说，天体质量越大，引力就越大；但两个天体之间距离越远，引力就呈指数级衰减。这样我们就好理解了，在地球表面的第一宇宙速度、第二宇宙速度、第三宇宙速度，随着距离地球表面的远离，是不断变化和衰减的，距离越远这些个速度要求就越小。

现在我们来说说第一宇宙速度，在地球表面为每秒7.9公里，也就是说在地球上起飞的物体，需要达到每秒7.9公里才能与地球引力对抗。但这个速度是摆脱不了地球引力的，只能是与地球引力取得一个平衡，既不被地球引力扯下来，也逃不掉地球引力的牵制，只能围着地球转。

因此，第一宇宙速度又叫环绕速度，其遵循的公式是根据牛顿万有引力定律变化而来，表述为v²=GM/r。这里的v表示环绕所需的速度，也就是所谓第一宇宙速度；G为引力常数，M为需要摆脱的天体质量，也就是地球质量；r为要摆脱地球质量的物体与地球引力中心，也就是地心的距离。

地球半径约为6371公里，可视为地心到地表的距离，根据这个公式，我们可以计算出在地球地表的第一宇宙速度。计算列式为：v^2=（6.67*10^-11）*（5.965*10^24）/6371000≈62449458，v≈7902米/秒。

这就是所谓第一宇宙速度的来源，如果有个物体飞行在距离地球表面2万公里的上空，所谓第一宇宙速度就只需要约3844米/秒了。而月球平均距离地球为38.4万公里，地球对其引力就弱了很多，根据环绕公式计算，其公转速度只要达到1018米/秒，就达到了环绕速度，这就是月球公转速度只达到约1.2公里，却不会被地球引力吸下来的原因。

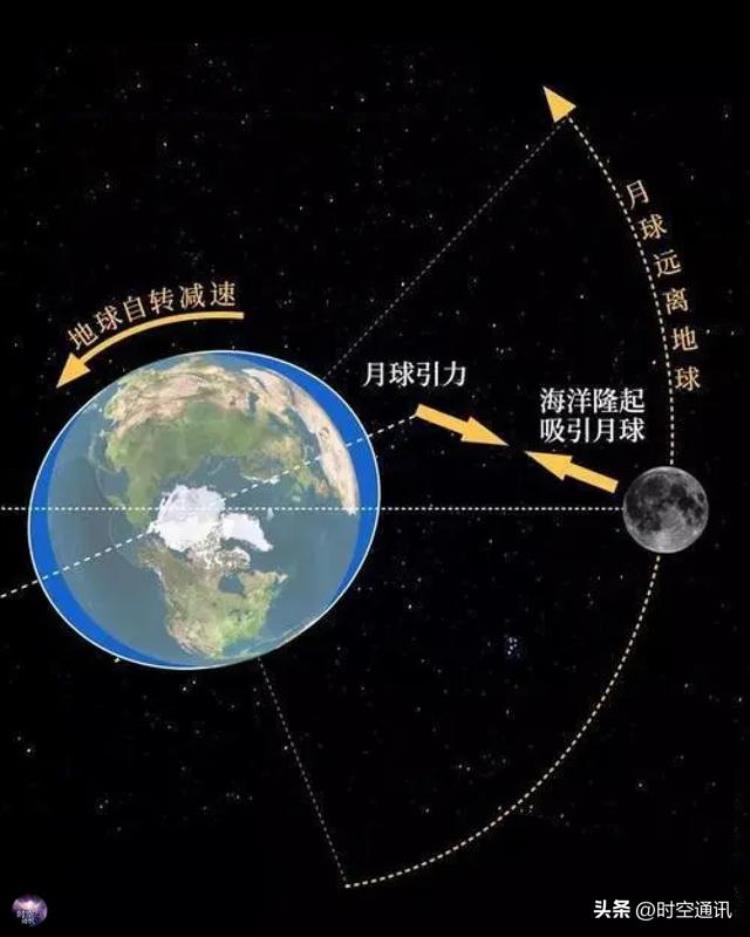
事实上，月球正在以每年3.8厘米的速度远离地球，其中的原因众说纷纭。有一种说法认为，这种现象主要由地月之间周期性潮汐作用产生，即月球的引力导致地球海水的潮起潮落，损耗了地球自转的能量，地球自转速度不断下降，从而导致月球逐渐远离。

但另一种说法认为，引力只与质量和距离有关，与自转快慢没有毛关系，导致月球逐渐远离的原因很复杂，并非某些人说的由于地球自转变慢问题。这是另外一个话题，说来话长，今天就不展开说了。

时空通讯原创版权，请勿抄袭侵权，感谢理解支持。

我在百度百科上看到，月球的平均公转速度是1.023千米/秒，这低于第一宇宙速度，那它为什么不掉下来？

以第一宇宙速度运转的人造地球卫星必须在近地轨道。只要是运动轨道半径大于地球半径的人造卫星的线速度都小于第一宇宙速度。地球同步卫星的线速度也小于第一宇宙速度，为3.2千米/秒。
它们在其轨道上运转时受到的万有引力恰好等于它们做匀速圆周运动所需要的向心力，所以月亮也和其它的卫星一样不会掉下来。

为什么月球公转只有1km/s,远低于第一宇宙速度,还没有被地球吸过来

因为月球本身已经就离地球很远（相对地面而言势能较高），所谓的第一、第二...宇宙速度是针对从“地面”即地球表面出发的物体而言的。
试想我们将一颗卫星送到和月球一样的轨道上，运送过程中本身是还需要很多能量的。