质量指标为什么用p表示「质量统计中P为什么饱受争议」
我们暂且把这个问题搁置一下,替P值君问一句:「为什么受伤的总是我呀?是我是我还是我」真要说起个问题,咱们得从统计学的框架说起。
现代统计学的框架
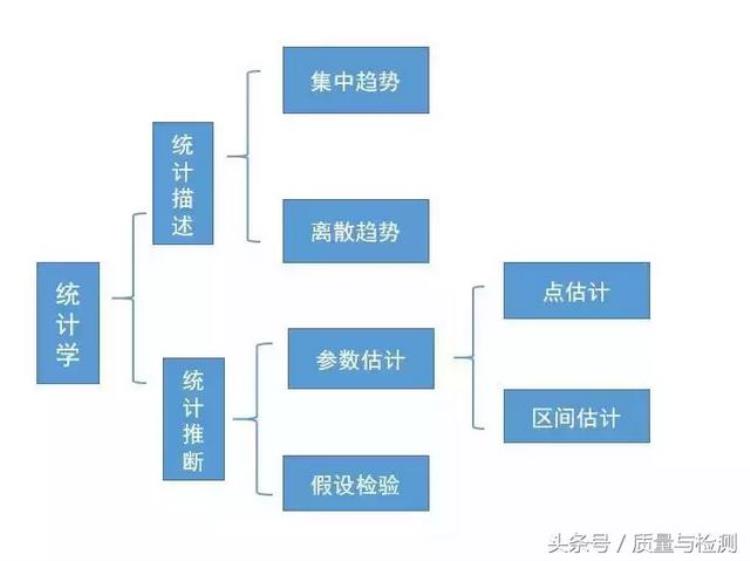
现代统计学两分天下:一分统计描述,一分统计推断。
统

也不知道P值是招谁惹谁了,反正大家都喜欢拿他开刷!老早就有一篇争议挺大的公众号文章说「P值已死」,立马就有人反驳「别闹了,P值没死」。其实, Nature杂志在14年2月份时就刊发了一篇文章,对统计效度的金标准「P值」提出了质疑,认为P值并没有统计学家所认为的那样可信。
我们暂且把这个问题搁置一下,替P值君问一句:「为什么受伤的总是我呀?是我是我还是我」真要说起个问题,咱们得从统计学的框架说起。
现代统计学的框架
现代统计学两分天下:一分统计描述,一分统计推断。
统计书上经常这样表述:
统计描述和统计推断是现代统计学的两个组成部分,两者相辅相成、缺一不可,统计描述是现代统计学的基础和前提,统计推断是现代统计学的核心和关键。
统计描述就是给数据拍张快照呗,看看他们长什么样子。我们熟知的均数、中位数就是用来看他们扎堆的位置,扎在什么地方;标准差、四分位数间距等就是用来看他们扎堆的程度,扎得有多紧。当然我们也可以用直方图,箱线图,散点图等统计图形来更为形象直观的查看。
统计推断是用我们手中的样本数据来推断其背后的总体特征。
统计推断里有两大块内容:参数估计和假设检验。
参数估计
就是我们用样本的统计量(如样本均数)去估计总体的参数(如总体均数)。此时,我们可以有两种策略:一种是简单了事,直接把样本统计量当做总体参数,这就是所谓的点估计;另外一种策略就是考虑到抽样误差,我们用一个范围,而不是一个单一的值去估计总体参数,此即所谓的区间估计。而假设检验则是利用小概率反正法思想,从问题的对立面(H0,原假设)出发,假定H0成立的条件下,去计算检验统计量,获得P值,再通过P值来在H0,H1(备择假设)之间做进一步取舍。
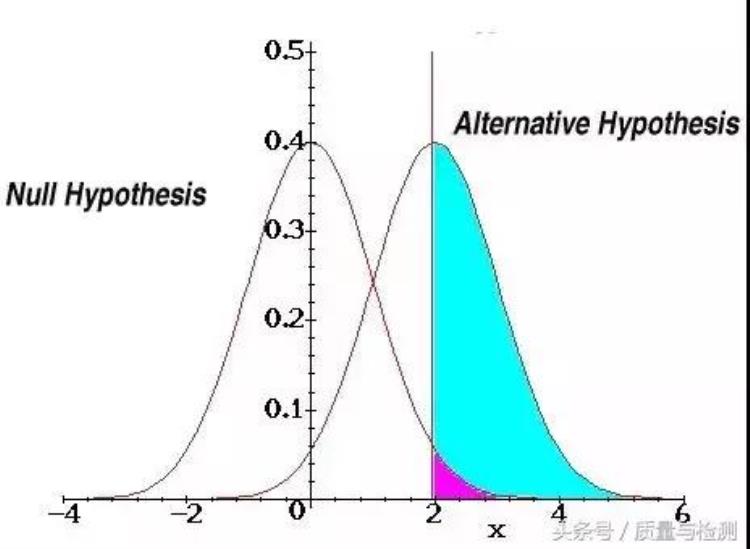
既然统计推断是现代统计学的核心和关键,看到这里,你也能体会到作为假设检验的黄金判定标准的P值,在统计学中的地位啦。那具体而言,什么是P值呢?
P值和假设检验
什么是P值呢?按照频率学派的经典套路:
敷衍的人会告诉你:「P值啊,就是P Value,Probability Value,就是概率啊」听完我们想揍死他,你还别笑,有些统计培训班还真这么讲的老实本分的老师会告诉你: 「P值啊,就是在H0为真的条件下,获得当前样本或者更偏的样本的概率」。听完我们很迷茫啊,看着我们迷茫的眼神,老师无奈的写下「P=Prob(X|H0)」,我们只好无奈且善意的点点头少有的明白人会告诉你:「P值啊,就是在H0为真时,观察到的差异来源于抽样误差的可能性大小」P值就是在H0为真时,观察到的差异来源于抽样误差的可能性大小。听完这个解释,或许我们眼前能闪现一丝灵光。我们以正态分布的Z检验为例简要说明下,不知道不理解为什么那么多的统计教材竟然要以t检验为例来讲假设检验。如果你被他们毒害了,不知道什么是Z检验,请看如下公式:
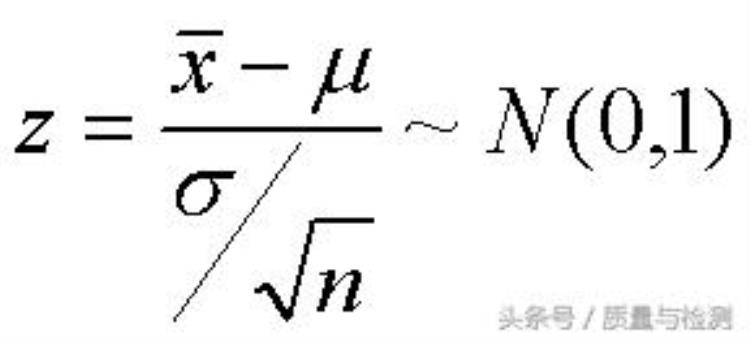
看不懂?不着急。一步一步来。依据「P值就是在H0为真时,观察到的差异来源于抽样误差的可能性的大小」这一定义,我们假定H0为真,也就是假定样本均数「X Bar」(即X头上抬根杠,微信编辑器什么时候能插入公式啊,只好拟音啦) 就等于总体均数「miu」(拟音),但是实际上,我们利用手中的样本数据计算的均数 「X Bar」和总体均数「miu」总是有差异的,这个差异就是公式中的分子,但是这个差异缺乏一个统一的度量,于是 我们除以一个 总体的变异幅度(暂且用标准误代替,也就是上图中的分母), 这样就得到一个以总体变异幅度来度量的差异,也就是说这个差异是多个标准误,或者说差了多少个标准误的距离,这个就是我们所说的统计量,Z值。现在在看看Z检验的公式,是否好容易理解多了? 统计量Z值其实就是样本均数和总体均数相差的,以标准误度量的单位量。
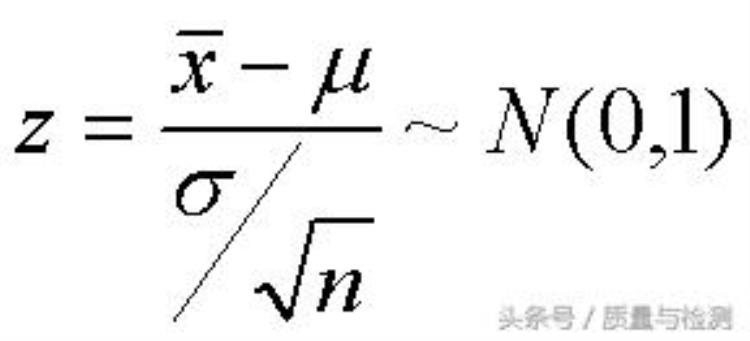
那么P值呢?别急。每一个Z值可以对应到一个相应的P值,比如,Z=1.96表示 差了1.96倍标准误的距离,对应的P 值就是0.05。
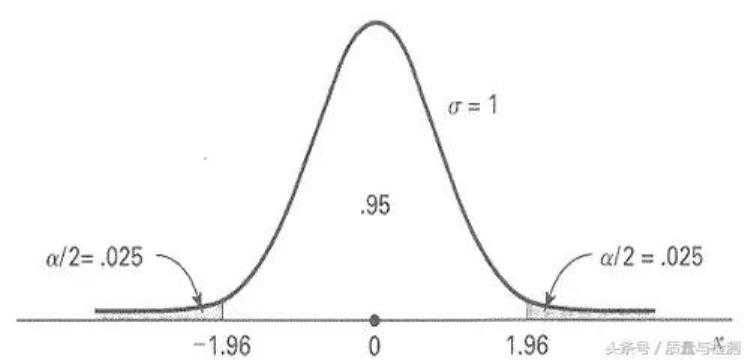
但是不同的分布,统计量不同,因此难以标化统一,不过P 值却可以,而且在实际操作中,由于计算机统计软件包的发展,P值也很容易获得。 获得P值后,比如,比如啊,P=0.003,我们可以回过头来想:既然我们已经假定H0为真了,也就是(「X Bar」-「miu」)应该没有差异了,但是现在还有Z倍标准误的差异啊! 那现在这个差异是哪里来的呢?只有一个可能的原因:抽样误差。但是现在可以归因于抽样误差的概率很小,只有0.003啊(统计软件计算结果),0.003的概率,1000次也才3次,竟然一次就让我们赶上了,这不太可能吧?是的,确实不太可能。那我们就只能回过头来怀疑我们的根基,我们的原假设H0错了,因此我们否定H0, 接受H1。
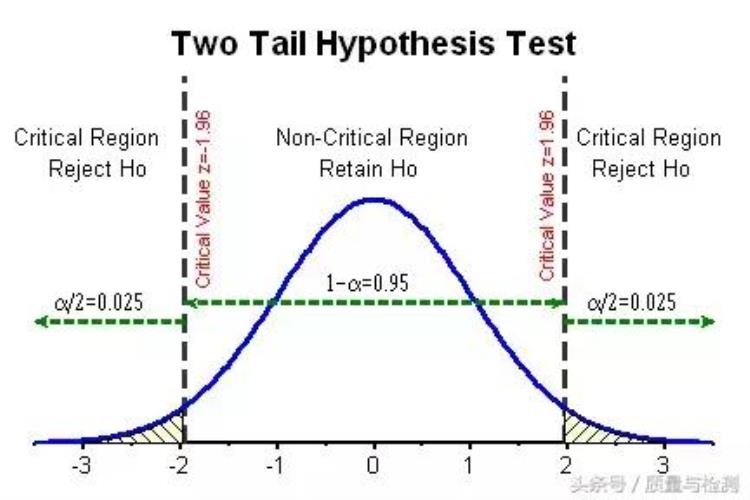
这才是我们的假设检验。这才是我们的P值。既然P值是假定H0为真的条件下,我们所观察到的差异来源于抽样误差的概率。这很容易让我们想到,如果H0真的为真,我们因P值
I类错误的概率是不是P值呢?To P or not to P, that's a question。 要说起清楚这个问题,还得劳神费心谈谈假设检验的前世今生。
其实,「前世今生」系列的文章我已经看到过好几篇了,比如「正太分布的前世今生」、「Meta分析的前世今生」。不知为何,我个人也很喜欢「前世今生」这个词。今天呢,就聊一聊我知道的一点「假设检验的前世今生」吧。
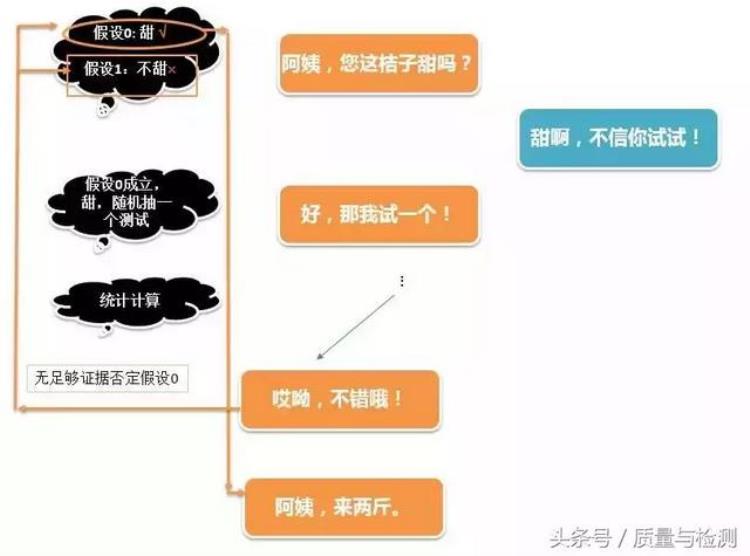
假设检验是统计学里最重要、最基础的的概念,即便是不知道,不了解这个术语,与统计学毫不相干的人,在日常生活中,也不知不觉地应用了假设检验。比如,我们在街上水果摊闲逛买橘子。
甜的时候,我们的思维过程:
不甜的时候,我们的思维过程:
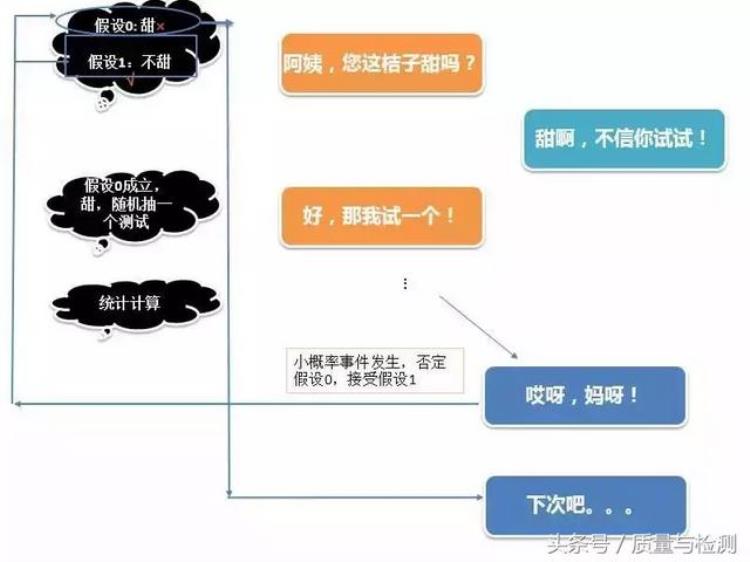
当然,以上只是个简单类比,不必细究。不过,相比一些翻译教材喜欢用老外的「法官定罪」的例子来说,这个场景应该更容易为国人所理解。
现行的假设检验,叫原假设显著性检验( Null Hypothesis Significance Testing,NHST)。其基本思路和框架在现行的统计教材中论述较多,在此仅简要概括:
建立假设,确定检验水平。假设包括两种,一种称为原假设、无效假设、零假设(Null Hypothesis,H0);另一种称为备则假设(Alternative hypothesis, H1),H1是H0的对立面。原假设H0通常是「别担心,啥事也没有」,比如没有差异,没有疗效等。H1 则是「有情况,要留意啊」,比如有差异,有疗效。检验水平alpha,又称显著性水平,这个是预先规定游戏标杆,通常为0.05。计算检验统计量,计算P值。我们认为手头已有的数据是从H0 为真的总体中的一个抽样,但是这个可能性是多少?这需要计算评估。如何计算评估呢?我们可以计算检验统计量,不过不同的问题,计算的检验统计量不同,如Z值,t值,F值,X2值,这样岂不是比较乱?是的,所以把那些统计量统统对应到P值,统一用P值来解决。做出统计推断结论。比较P值及alpha值,如果 Palpha, 不拒绝H0,差异不显著,无统计学意义。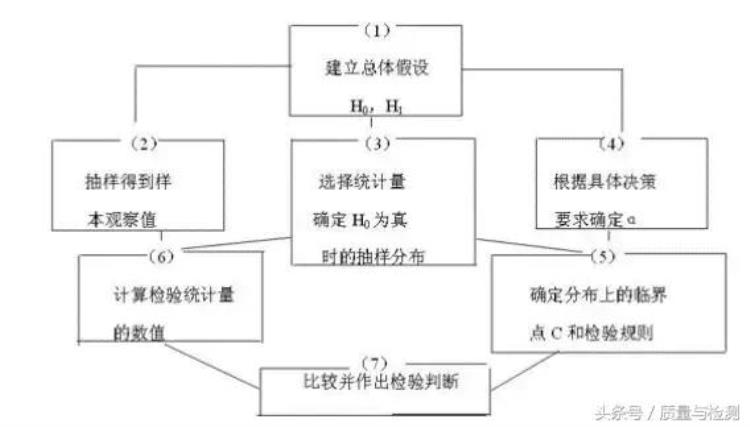
不太想了解假设检验的具体流程和细节的,只要记住一条简单粗暴的黄金口诀:If P is low, H0 must go!
以上这一套流程,看起来好像是流畅统一的整体,然而,统计教材没有说明的是,这其实是一道大拌菜,是统计学家Karl Pearson的「拟合优度检验」,Ronald A Fisher的 「显著性检验 」和 Jerzy Neyman,Egon Pearson的N-P「假设检验」的大杂烩。
故事的关键点大概是这样的:
Karl Pearson的「拟合优度检验」
部分文献以为P值是Fisher发明的,但其实最先提出P值的是Karl Pearson。Karl Pearson在其1900年的论文中提出了拟合优度的卡方检验,这其中就包括P值。但是给出了P值的在各种情形下的计算方法的却是Karl Pearson的死对头,Ronald A Fisher。应该说,Karl Pearson的提出了「P值 」,Ronald A Fisher 将「P值 」发扬光大。 而1925年Ronald A Fisher的 经典著作《Statistical Methods for Research Workers》腾空出世奠定了其现代统计学之父的威名。

Karl Pearson
Ronald A Fisher的 「显著性检验 」
1925年,Fisher提出了其显著性检验的思想。Fisher的显著性检验可大概概括为以下5个步骤:
选择合适的检验,如卡方检验,t检验建立原假设H0假定H0的条件下计算理论的P值评估结果是否有统计学显著对结果的统计学显著性进行解释
Ronald A Fisher
N-P的「假设检验」
1928年,Jerzy Neyman和Karl Pearson 的儿子 Egon Pearson提出了「假设检验」,「假设检验」思想可大概概括为以下8个步骤:
设立人群中期望的效应值选择合适的检验建立主假设Hm建立备则假设Ha计算为达到良好的把握度所需的样本量计算检验的临界值,确定拒绝域计算研究的检验值(老实说,这条我也没理解)做出支持Hm或者Ha的决策
Egon Pearson,Jerzy Neyman
简单来看,Ronald A Fisher的 「显著性检验 」是没有备则假设的,而N-P的「假设检验」不仅有备则假设,还有一个主假设Hm(与H0类似),不仅如此,N-P的「假设检验」还提出了效应值、把握度,I类、II类错误的概念,且采用拒绝域而非P值来做决策。
除了以上形式上的差别,Ronald A Fisher的 「显著性检验 」与N-P的「假设检验」在深层次的统计哲学上也不同。
Fisher的统计模型的方法论基础是假想无限总体,现有资料可视为是从中抽取的一个随机样本。而N-P则是假想无限抽样。N-P 「假设检验」 的要旨为在限制第一类错误的概率不超过显著性水平 α 的条件下, 谋求第二类错误的概率最小化。虽不期望知晓每个独立的假设是真是假, 但仍可研究指导我们与之相关行为的准则, 以便保证在长远意义上不至错得太多。Fisher认为统计学的功用是“归纳推论” ( inductive inference) , 而不是做“归纳行动” ( inductive behavior) ; 统计学应当止于归纳结论, 而不涉足行动判断。显著性检验不能给出针对现实的判断, 而只能改变研究者对事实的态度。而在 N-P 看来, 没有任何一种统计推论思想能够不涉及决策过程。他们直接绕过假设检验作为科学推论的适合性的讨论, 而将它作为一种决策方法, 在先行给出决策前提( 控制第一类错误、 然后追求功效最大化) 的前提下, 进行数学上的最优化论证( 错误率最低) 。这种思维方式对实际研究者显然是很有“实际优势” 的, 因为这正符合了他们使用假设检验的最初目的和最终期待原假设显著性检验,NHST
1940年,Lindquist首次对Ronald A Fisher的 「显著性检验 」和N-P的「假设检验」进行了糅合, 提出了原假设显著性检验(Null Hypothesis Significance Testing, NHST)。
NHST 的基本杂合方式是:
采用 N-P 的原假设对备择假设 的假设形式( H0 vs H1) , 而备择假设却是 Fisher 没有使用并且一直反对引入的 同时采用 P值( Fisher 的判断依据) 和拒绝域法( N-P 的判断依据) , 认为两者的判定效果是等价的, 但 Fisher 本人却极其反对拒绝域法, 而 N-P 则并不强调P值的作用把检验功效 和两类错误作为 NHST 的内在内容加以介绍, 而不提及这只是 N-P 的观点, Fisher本人是反对这些概念的。至此,这就是我们统计教科书里看到的假设检验了。NHST自其诞生以来就饱受质疑和批判,后世的统计学家也一直在呼吁用置信区间,贝叶斯统计来取代NHSTH这种统计推论方式。更多批判NHST的文章和更深层的讨论,好像已经超出我的能力范围了。


文章评论