WorkwithGPT(2)实验分析中经常使用的统计知识

GPT强大的知识涉猎、结构化整理能加速大家的学习过程，后面后通过专业领域上的深入来展开如何用GPT做我们的副驾（Copilot）协同我们的工作

GPT给出关键的概念

Q1：实验分析中经常用的的统计学知识

A1：

在实验分析中，经常使用的统计学知识包括：

假设检验：用于确定实验结果是否显著，通常会计算P值来判断实验结果是否出现偶然误差。置信区间：用于确定实验结果的不确定性范围，通常在结果报告中展示置信区间可以提供更加准确的数据分析结果。样本大小：用于确定实验需要的样本量，通常需要通过统计学方法来计算。效应量：用于确定实验结果的大小和重要性，通常会使用Cohen's d、r、Eta-squared等指标来计算效应量。多重比较校正：用于控制实验中多次比较产生的误差，通常会使用Bonferroni、Holm-Bonferroni等方法来控制多重比较的误差。分布假设：用于确定实验数据的分布情况，通常会使用正态分布、t分布、F分布等分布假设来进行实验数据的统计分析。

以上是实验分析中常用的统计学知识，可以帮助数据分析师更加准确地评估实验结果，并提供更加可靠的数据分析报告。

让GPT给你举个例子

Q2：展开介绍下上面的知识，并通过一个实验例子演示下如何进行计算

A2：

好的，让我们通过一个简单的实验来演示一下如何应用实验分析中经常用到的统计学知识。

假设我们是一个电商网站的数据分析师，我们正在评估一个新设计的网站首页是否能提高用户购买率。我们决定进行一个 A/B 测试。我们将把网站的用户随机分为两组，一组将看到旧版的网站首页（组A），另一组将看到新设计的网站首页（组B）。我们会跟踪每个用户的购买行为，并记录每组的购买率。

现在我们已经收集了足够的数据，我们得到了以下结果：

组 A：1000 个用户中有 50 个购买了商品，购买率为 5%组 B：1000 个用户中有 80 个购买了商品，购买率为 8%

接下来，我们需要进行统计学分析来确定这些结果是否具有显著性。在这个例子中，我们可以采用以下步骤：

假设检验：首先，我们需要确定我们的零假设（H0）和备择假设（H1）。在这个例子中，我们的零假设是“组 A 和组 B 的购买率没有显著差异”，而备择假设是“组 A 和组 B 的购买率存在显著差异”。显著性水平：接下来，我们需要选择显著性水平。显著性水平是指我们拒绝零假设的程度。通常，我们会选择 5% 的显著性水平。统计检验：我们可以使用 t 检验来计算我们的样本差异是否显著。在这个例子中，我们可以使用独立样本 t 检验来比较两组之间的购买率。t 检验需要计算 t 值，以及自由度和 P 值。计算 t 值：使用以下公式计算 t 值：t = (mean(B) - mean(A)) / (s / sqrt(n))其中，mean(A) 和 mean(B) 分别表示组 A 和组 B 的购买率，s 是两组样本的汇总标准差，n 是每组的样本数。在这个例子中，我们可以计算出 t 值为 2.51。计算自由度：使用以下公式计算自由度：df = nA nB - 2其中，nA 和 nB 分别表示组 A 和组 B 的样本数。在这个例子中，自由度为 1998。计算 P 值：最后，我们可以使用 t 分布表或统计软件计算 P

例子已经足够详细，个别概念如果不理解，可以追问GPT。

不断地追问

Q3：上面例子中购买率分别为5% 8%，如何计算t值？有几种方法？

A3：

假设样本量相等，即 A 组和 B 组的样本量相同，设样本量为 n，A 组有 a 个转化，B 组有 b 个转化，A 组和 B 组的转化率分别为 pA 和 pB。

则 t 值的计算公式为：

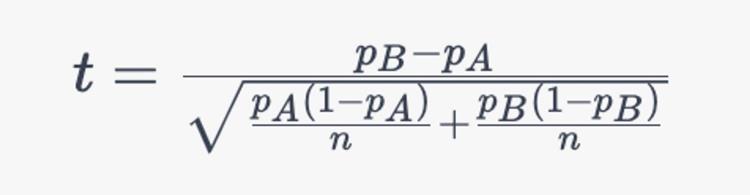
对于上述例子，样本量为 1000，A 组有 50 个购买，B 组有 80 个购买，A 组的购买率为 5%，B 组的购买率为 8%。将这些值代入公式中可得：

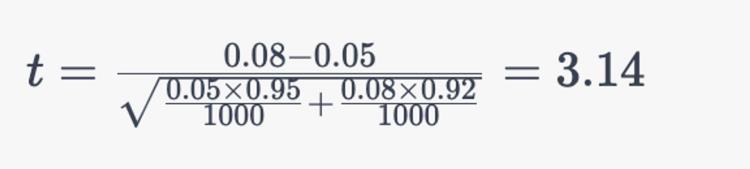
这里只介绍了一种计算 t 值的方法，另外还有基于置信区间和假设检验的方法。在实验分析中，可以根据实际情况选择合适的方法进行 t 值计算。

继续追问

Q4：还有哪些t检验的方法？

A4：

除了上述两种t检验，还有配对样本t检验和单样本t检验。

单样本t检验用于检验一个样本的平均值是否与某个已知的值相等。计算公式为：

t = (x̄ - μ) / (s / sqrt(n))

其中，x̄ 是样本的平均值，μ 是要检验的已知值，s 是样本标准差，n 是样本大小。

配对样本t检验用于比较两个相关的样本的平均值是否有显著差异。例如，在比较同一组人的体重在某个干预前后的变化时，就需要进行配对样本t检验。计算公式为：

t = (d̄ - μd) / (sd / sqrt(n))

其中，d̄ 是配对差值的平均值，μd 是要检验的已知值，sd 是配对差值的标准差，n 是配对样本的大小。

需要注意的是，在进行t检验之前，要检验数据是否符合正态分布假设，并进行方差齐性检验，选择合适的t检验方法。

答案引发新的追问

Q5：如何进行方差齐性检验

A5：

方差齐性检验是检验两个或多个总体方差是否相等的一种方法，通常在进行 t 检验、方差分析等统计方法时需要进行方差齐性检验。以下是两种常用的方差齐性检验方法：

Levene's test：该方法将数据分组并计算每个组的方差，然后比较不同组之间方差的大小，检验它们是否相等。在 Python 中，可以使用 Scipy 的 levene 函数进行计算。Bartlett's test：该方法也是将数据分组并计算每个组的方差，但它比较不同组之间方差的大小时采用的是卡方分布，可以处理非正态分布的数据。在 Python 中，可以使用 Scipy 的 bartlett 函数进行计算。

需要注意的是，方差齐性检验的结果是对 t 检验、方差分析等后续统计方法的影响，如果结果显示方差不齐，则需要使用相应的调整方法，如 Welch's t 检验、Welch–Satterthwaite 方差分析等。

然后可以逐步探索了解如何进行Welch’s T检验，如何进行多重比较修正、方差缩减等等。