一元二次求根公式（编写函数求一元二次方程的根）

解一元二次方程的方法有很多，比较常见的有公式法、配方法和因式分解法。其中公式法适用一切一元二次方程，且比较简单，只要牢记求根公式就可以了。求根公式如下：

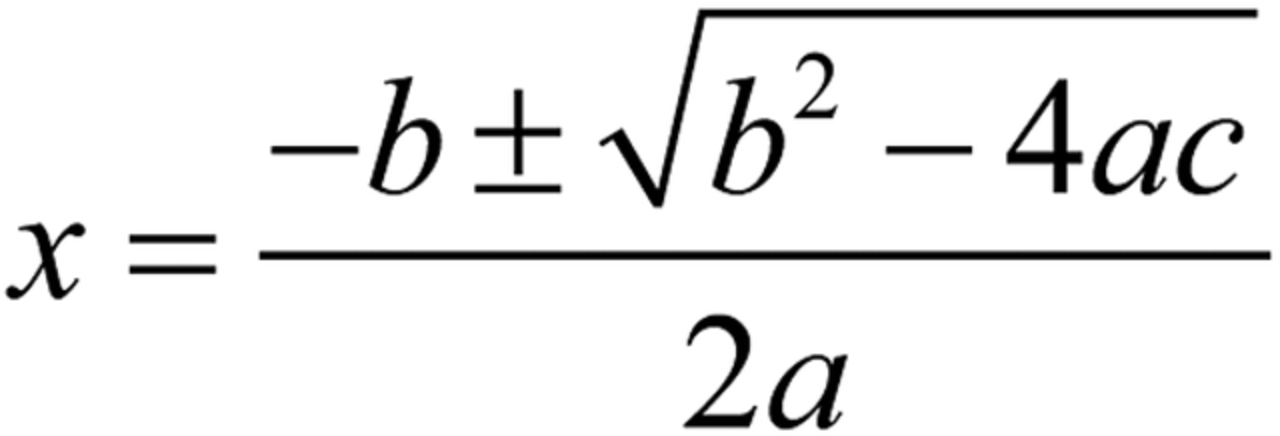
这个求根公式是针对一元二次方程的一般式ax^2+bx+c=0得到的。然而简单的死记硬背虽然能够把公式记牢，但却不是一种好办法。我们还要分析公式的结构、来源、应用以及拓展，这样才能真正形成数学能力，不仅能够巩固掌握公式的应用，还能融入自己的知识体系，既省力又高效，在以后的练习中才能灵活地应用。

在运用公式法时，未必要使用完整的公式。其中b^2-4ac又称为一元二次方程的判别式，常用表示。判别式的符合性质决定了一元二次方程根的情况：

当<0时，一元二次方程是没有实数根的，这时在实数范围内，就不需要继续运用完整的公式去求根了，只需要说明“方程没有实数根”就可以了。

当=0时，一元二次方程有两个相等的实数根，因为0的平方根仍是0，因此方程的根是x=-b/(2a)，正好是对应的抛物线y=ax^2+bx+c的对称轴的形式。

只有当>0时，一元二次方程有两个不等的实数根，才需要用到整个求根公式。这时只要把方程的三个参数代入就可以了。但是千万要注意，对于关于x的一元二次方程bx^2+ax+c=0或者ax^2-bx+c=0，直接用求根公式表示它的根却是完全错误的。这就要涉及到求根公式的来源了。

求根公式其实是对一元二次方程的一般式ax^2+bx+c=0运用配方法求根得到的结果。有多少学生会自己动手去进行这番操作呢？只要自己动手推出过求根公式，就能过明白求根公式的实质，以后就不会出现乱用求根公式的情况了。

另外，因式分解法的实质，其实也与求根公式有关，记x1,x2表示求根公式的两个不同的结果，将一元二次方程ax^2+bx+c=0进行因式分解，就是把方程写成(x-x1)(x-x2)=0的形式。这样就不仅能在有理数的范围内进行因式分解，还可以在无理数的范围内进行因式分解了。

最后，一元二次方程的根与系数的关系，x1+x2=-b/a，x1x2=c/a，即韦达公式，其实也是由求根公式推出来的，你知道吗？动手自己推导一下，你肯定能在数学中找到更多乐趣的。